Paradacsa Simpson
Is paradacsa é Paradacsa Simpson a bhaineann le saobh-comhghaolú (spurious correlation) sa staidreamh agus mí-chruinneas san réasúnaíocht.
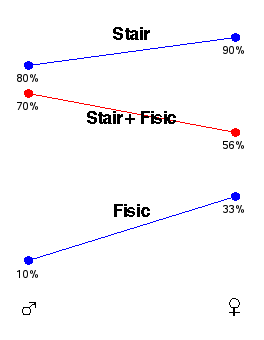
Tá ollscoil ann, ina n-éironn níos fearr ag na cailín i ngach dámh, ach ar an iomlán, tá na buachaillí níos fearr. Mar shampla, sa Stair, tá ráta pas, sna scrúdaithe, de 90% ag na cailíní, i gcomparáid le 80% dos na buachaillí. Is mar an gcéanna é sa bhFisic – cailíní (33%) agus buachaillí (10%).
Ag braith ar an eolas sin, tá sé réasúnta a ghlacadh go bhfuil ráta pas na gcailíní san ollscoil (níl ach an dá dhámh Stair agus Fisic ann) níos fearr ná an ráta dos na buachaillí. Ach a mhalairt atá, mar tá ráta pas na mbuachaillí (70%) níos mó ná ráta pas na gcailíní (56%).
Nuair a iniúchaimid na figiúírí i Tábla 1, tá sé soiléir go bhfuil an mhatamaitic ceart agus go raibh dul amú orainn.
Tagann na rátaí pas san ollscoil ón meán ualaithe (weighted mean) mar seo a leanas
Buachaillí [600@80% + 100@10%] / [600+100] = 70%
Cailíní [200@90% + 300@33%] / [200+300] = 56%.
Is léir ón bhFigiúr go n-iompaíonn na meánrataí idir buachaillí agus cailíní sa chaoi is go bhfuil an ráta do na buachaillí san ardréim.
Tá mí-chrothromaíocht sna ualaigh – an líon is mó de na buachaillí ag dul leis an ráta is mó agus formhór na gcailíní ag dul leis an ráta is lú agus tá bearna an-mhór idir na rátaí pas sa Stair sa don bhFisic. Is rud neamh-ghnáthach é seo. I staidéar [1] ar táblaí (2 x 2 x 2) mar atá anseo, tá dóchúlacht de 1/60 go mbeadh an dáileadh idir na tréithe ionas go sásófaí coinníollacha paradacsa Simpson (faoi choinníollacha áirithe).
Scríobh Edward H. Simpson,[2] faoin ábhar seo i 1951, ach bhí sé ar eolas ag staitisteoirí roimhe sin. Mar shampla Karl Pearson, et al., i 1899,[3] agus Udny Yule, in 1903[4] .
| Dámh | Scrúdú | Buachaillí | Cailíni |
|---|---|---|---|
| Stair | Pas | 480 | 180 |
| Teip | 120 | 20 | |
| Pas+Teip | 600 | 200 | |
| Ráta Pas | 80% | 90% | |
| Fisic | Pas | 10 | 100 |
| Teip | 90 | 200 | |
| Pas+Teip | 100 | 300 | |
| Ráta Pas | 10% | 33% | |
| Stair + Fisic | Pas | 490 | 280 |
| Teip | 210 | 220 | |
| Pas+Teip | 700 | 500 | |
| Ráta Pas | 70% | 56% |
Tagairtí
cuir in eagar- ↑ Marios G. Pavlides and Michael D. Perlman (August 2009). "How Likely is Simpson’s Paradox?". The American Statistician 63 (3): 226–233. doi:.
- ↑ Simpson, Edward H. (1951). "The Interpretation of Interaction in Contingency Tables". Journal of the Royal Statistical Society, Ser. B 13: 238–241.
- ↑ "Genetic (reproductive) selection: Inheritance of fertility in man" (1899). Philosophical Translations of the Royal Statistical Society, Ser. A 173: 534–539.
- ↑ G. U. Yule (1903). "Notes on the Theory of Association of Attributes in Statistics". Biometrika 2: 121–134. doi:.